Search
Menu
All issues Volume 5 (2017) EPJ Nonlinear Biomed. Phys., 5 (2017) 1 Full HTML
Open Access
Issue
EPJ Nonlinear Biomed. Phys.
Volume 5, 2017
Article Number 1
Number of page(s) 9
Section Physics of Biological Systems and Their Interactions
DOI https://doi.org/10.1051/epjnbp/2017000
Published online 24 May 2017

© L.W. Sheppard et al., published by EDP Sciences, 2017

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

In biophysical systems, multivariate data is often autocorrelated and cross correlated and incorporates a spectrum of fluctuations on different timescales. A coherence measures the tendency for a particular phase relationship to exist between fluctuations in two signals, and can illustrate how this relationship varies with frequency. For finite data, spuriously high coherence can arise where there are correlations between successive phase measurements [1].

A continuous wavelet transform can be applied to any signal to extract phase values corresponding to fluctuations with different timescales. Biophysical examples include blood flow and temperature fluctuations in human skin subject to heating and cooling [2], fluctuations in human blood pressure and skin conductivity during anaesthesia [3], and the intracranial pressure and arterial blood pressure in subjects with a traumatic brain injury [4]. Wavelet transforms and related methods have also been applied to study phase relationships in ecology [5–9]. As an example of a complex biophysical system described by spatiotemporal data incorporating frequency-dependent phase shifts, we examine the annual changes in the abundance of different plankton species in the seas around the British Isles since 1958. Pioneering work using Fourier methods [10] showed a phase shift between the fluctuations in phytoplankton productivity and sea surface temperature.

We define a wavelet coherence as an average over time of a complex quantity with a phase representing the phase difference between transforms of two timeseries, at a particular time and timescale. The magnitude of this average therefore represents the tendency to preserve a particular phase difference over time, and the phase is the typical phase difference that is preserved. The wavelet coherence is analogous to a correlation coefficient, but maintaining the advantages of frequency specificity and retention of explicit information about phase.

Coherence statistics are closely related to directional statistics, particularly in the case of the wavelet phase coherence [11]. To compute the wavelet phase coherence, the amplitude variability of the wavelet components is removed from consideration and the coherence is calculated using normalised unit phasors representing the phase values extracted from the wavelet transforms at each point in time. The phase coherence is equal to one minus the circular variance of the phase difference (calculated across time) [12]: both are measures of the tendency to preserve a fixed phase difference. Equivalently, the circular variance is a measure of the spread of values in a circular distribution, and the phase coherence a measure of the tendency to cluster around a single modal value. The same biases arising from non-independence of successive phase values arise in both measures.

Where pairs of timeseries are available from several spatial locations or measurement sessions, we can generalise to a spatial wavelet phase coherence. We calculate a spatial coherence [8] by taking an average over both times and locations. The magnitude reflects the tendency to preserve the same phase difference at all times and locations, and the phase is this typical phase. Having data from many locations increases the ability to pick out a typical phase in partially coherent systems, but requires careful statistical testing. If the timeseries being compared are themselves spatially correlated, then measurements of the phase differences found between them at the different locations are non-independent.

Methods of generating artificial surrogate data [13,14] are commonly used to test whether particular coherence values are likely to occur under the null hypothesis of no relationship between variables. Surrogates based on Fourier transforms of the data preserve its spectral properties to make a fair test. Reference [15] defines a procedure for generating surrogates of several timeseries (e.g., timeseries representing the same variable measured at several sites simultaneously) while preserving their cross spectra. We refer to these as spatially synchronous surrogates; such surrogates are required to test the null hypothesis that two sets of timeseries taken from the same set of locations are themselves spatially correlated but no relationship exists between them.

Different patterns of frequency dependent phase relationship occur for different kinds of dependent system, so detecting phase relationships may illuminate the nature of the dependence. We give five examples. First, correlation and anti-correlation are equivalent to a 0-radians phase shift and a π-radians phase shift, respectively. Secondly, autoregressive moving average (ARMA) models [16] can produce diverse patterns of frequency dependent phase relationships. If we wish to represent a variable x(t) by an ARMA model, multiplying the spectral components of a driver h(t) by a complex factor (the transfer function), this factor must be frequency dependent in both amplitude (gain) and phase. The frequency specificity of the relationship between variables in the kinds of models that occur frequently in biological and nonlinear systems motivates us to test for frequency specific coherence, using time-frequency methods. Thirdly, synchronization of periodic oscillators by small phase adjustments can produce extremely high coherence at their oscillation frequency [17]. Fourthly, combination of different periodic processes in the same time series [18] can produce distinct phase relationships at the different periods involved. Fifthly, rate dependencies: sometimes the value of one variable depends on the rate of change of another, or vice versa. Because d sin (ωt)/dt = ω cos (ωt), either differentiating or integrating any time series represented by a sum of sinusoids with respect to time produces another sum of sinusoids, with a positive or negative π/2 phase shift and a gain proportional or inversely proportional to frequency. Figure 1a presents the phase shift between the Morlet wavelet components of sample Gaussian white noise h(t) and the first difference of h(t), compared to the typical phase difference between h(t) and the cumulative sum of h(t), as determined by the wavelet phase coherence approach. Figure 1b shows the wavelet power of h(t), its first difference, and its cumulative sum. We see that the lowest-frequency components of either the first difference or cumulative sum are shifted by a quarter cycle relative to h(t). The higher the sampling frequency relative to the frequency of interest, the closer the first difference and cumulative sum operations come to producing a π/2 shift at that frequency.

Because coherence methods are common and useful but require computationally intensive significance testing, and because coherence methods are increasingly used with spatial data and/or in complex multi-variate systems, there is a need to develop a faster significance testing method. We here provide one. Sections 2.1–2.3 describe the method. Sections 2.4 and 3 describe an application to complex ecological data that would be difficult or impossible without the computational speed-up achieved by the new method. Section 4 concludes.

thumbnail Fig. 1

(a) Phase shift of wavelet components of the first difference of h(t) relative to h(t), in blue, and phase shift of wavelet components of the cumulative sum of h(t) relative to h(t), in red. Black lines are at π/2 and −π/2. (b) The driver, h(t), is white noise, with a power spectrum shown in green (the area under the curve represents the wavelet power in a spectral interval), while the power spectrum of the first difference of h(t) is shown in blue and that of the cumulative sum is in red.

2 Methods

2.1 Wavelet coherence, spatial wavelet coherence, and spatial surrogates

Wavelet phase coherence [11] is computed at each frequency by extracting only the phase values, ϕk,σ(t), at scale σ at each time t from t = 1 to t = T, from two wavelet transforms indexed by k = 1, 2 [19]. The phase difference is ϕσ(t) = ϕ1,σ(t) − ϕ2,σ(t).(1)(2)This magnitude is the phase coherence, and the phase of the summation tells us the phase difference that is maintained (on average) between these components. Wavelet phase coherence can also be written(3)

We can define a wavelet coherence to include the time-varying magnitudes of the wavelet components, wk,σ(t) = Ak,σ(t)eiϕk,σ(t),(4)We can significance test this quantity by comparison with the magnitude of the same dot product obtained for the transforms of surrogate timeseries. If there is correlated amplitude variability in the transforms this will tend to enhance the wavelet coherence relative to the wavelet phase coherence. However, correlated amplitude variability alone cannot produce high wavelet coherence; the oscillations themselves must maintain a particular phase relationship. Sensitivity to amplitude dynamics, and mathematical properties that make the wavelet coherence suitable for efficient surrogate testing, make the wavelet coherence a useful way of quantifying frequency-dependent associations in data.

Here and throughout we perform an average over all T values in the transform at a given frequency. Coherence measures can also be calculated inside a moving window, or by means of a convolution in the time domain with some weighting function such as a Gaussian. In this paper we focus on significance testing the tendency to maintain coherence over all time rather than within such a window.

Where transforms wk,n,σ(t) are available of data from several locations, indexed by n from 1 to N, we can define a spatial wavelet coherence,(5)and this quantity can be significance tested by the use of spatially synchronous surrogates [8].

2.2 Wavelet scalloping and false negative results

When calculating wavelet coherence of time series, one standard way to calculate the needed wavelet transforms is by the following method [20]. Denote one of the time series by x(t) for t = 1, … , T, and denote the wavelet of scale σ by , where σ = s/f0 and f0 = 1/2 (we use the complex Morlet wavelet [19], see Supplementary Material, Appendix S1). Let be the time series obtained by: (1) sampling ψσ(t) at integer values of t; (2) throwing away the t for which the Gaussian envelope is less than 0.1% of its maximum value; (3) defining L to be the positive integer such that there are 2L + 1 values remaining at this point; and (4) padding with T zeros on the right so the final time series has length 2L + 1 + T. Denote by x′(t) the sequence obtained by padding x by 2L + 1 zeros on the right. The wavelet component is an (appropriate) stretch of T of the values from the convolution . For computational efficiency, the convolution is carried out indirectly (but still exactly) using the convolution theorem (see [21], pp. 29 and 36): it is , where DFT is the discrete Fourier transform and IDFT is its inverse. The reason for zero padding is to make this rapid DFT-based computation equal to the (non-circular) convolution of the original, un-padded time series. Scalloping can be performed to remove poorly estimated values at the edges of the resulting time series, for which the wavelet substantially overhangs the edge of x(t) and the resulting convolution value is overly influenced by the added zeros.

We adopt a slightly different approach. The (continuous) Fourier transform of ψσ(t) is known analytically: 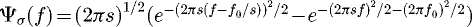. The product DFT(x(t))(f)Ψσ(f) is evaluated and is taken as the DFT of the desired wavelet component. In fact the wavelet component itself is never needed for our wavelet coherence surrogate testing algorithm (see Sect. 2.3), so is not computed; but because of the lack of zero padding, it essentially amounts to a circular convolution of x(t) with the wavelet (making use again of the convolution theorem), instead of the usual non-circular convolution. Scalloping could be performed in the usual way to remove values at the edges of the component, for which the wavelet substantially overhangs the edge of x(t) and the resulting circular convolution value is overly influenced by the other end of the time series. Via the standard approach, scalloping removes values unduly influenced by zeros; via the modified approach, scalloping, if performed, would remove values unduly influenced by the use of circular convolution.

In addition to providing computational benefits (see Sect. 2.3), our approach is not only acceptable for our application of wavelet coherence testing, it also reduces false negative rates for detecting significant coherence. When testing the significance of the coherence found between two transforms, accurate evaluation of the ‘true’ coherence is not the goal. The aim is to determine whether significant coherence exists at all by comparison to surrogate coherence values subject to all the same biases. Even edge values, which contribute considerable bias to the coherence of both the actual and surrogate transforms, also contribute information about the actual tendency to maintain a phase relationship in the data itself. We used admixtures of noise time series to examine false positive and false negative rates for detecting significant wavelet coherence via the standard method and via our method. We first used unrelated simulated time series xn(t) and yn(t) for n = 1, … , 20 and t = 1, … , 35. Data were standard normal and were independent across time, locations, and variables. The coherence at a given wavelet transform frequency was declared to have passed the test for statistical significance if it was greater than 95% of the surrogate coherence values. Rates of detection of ‘significant’ wavelet coherence (these were false positives) for both the standard and new algorithms were similar (Fig. 2a). We then used xn(t) = εn(t) and yn(t) = δn(t) + 0.15εn(t) for εn(t) and δn(t) standard normal and independent across time, locations and variables. Failures to detect the relationship between xn(t) and yn(t) (these were false negatives) were fewer for the new algorithm (Fig. 2b). False positives are no higher for the new algorithm, apparently because bias introduced by edge effects is present in both actual and surrogate transforms. Failed detections (false negatives) were slightly fewer for the new algorithm, apparently because useful information about phase relationships is in the edge values of transforms and is discarded by the usual approach.

We next show how unscalloped transforms based on circular convolution can lead to fast, intuitive determination of the significance of coherence measures. Having tested for significance, the original, less biased wavelet coherence based on scalloped transforms and non-circular convolution can be used to calculate coherence, with confidence that it represents a genuine relationship.

thumbnail Fig. 2

The false positive rate obtained at each frequency for tests of wavelet coherence based on independent data (a); and the false negative rate for an example of partly correlated data (b). The standard wavelet coherence algorithm is in red; the new, fast algorithm using circular convolutions and no scalloping is in green. Rates are based on 1000 simulations. Tests are based on 1000 surrogate data sets for each. See text for additional details.

2.3 Outline of approach to efficient calculation

The following steps used to calculate standard surrogate wavelet coherences are shown in Figure 3. The calculation of Fourier surrogates (box A) requires a Fourier transform operation on the data (step 1), a random rotation of the phases of the Fourier components (step 2), and an inverse Fourier transform to recover a Gaussian-distributed surrogate timeseries (step 3) [14]. If a correlation or phase relationship existed between the original signal and another signal, the relationship will not exist between the surrogate timeseries and that signal. The most efficient calculation (Sect. 2.2) of a continuous wavelet transform (box B) involves a Fourier transform of the timeseries (step 4), ‘filtering’ in the frequency domain using the Fourier transform of the wavelet corresponding to a given scale (step 5), and then inverse Fourier transforming to obtain a series of complex values corresponding to the wavelet transform of the timeseries at that scale (step 6). Finally, conjugate wavelet transform components of the second variable are combined via a kind of dot product (Eq. (4)) with the results of step 6 to produce the desired surrogate coherences (step 7, box C).

Some efficiency gains are immediate. Step one is the same for every surrogate and need only be performed once. Steps 3 and 4 are inverses of each other under the approach described in Section 2.2, and can be dropped.

Efficiency gains are also possible in steps 6 and 7. In step 7, one is computing the time-average quantity in equation (4), i.e. the time average of . But by Parseval's theorem (see [21], pp. 29 and 36), the time average of equals the frequency average of , up to a constant scaling factor. Thus step 6 can be dropped, and step 7 replaced by a dot product operation in the Fourier domain.

In Figure 3 we see the standard and optimised algorithms for calculating surrogate wavelet coherences. The most computationally intensive steps (requiring calculation of Fourier series) are marked in red. In the standard approach on the left, routine A (calculation of a Fourier surrogate), routine B (calculations of the surrogate's wavelet transform), and routine C (evaluation of the surrogate coherence) must be performed for every surrogate. In the efficient approach on the right, only routine D is repeated for every surrogate (see Supplementary Material, Appendix S2).

The three preliminary steps shown requiring calculation of Fourier series in the efficient approach are the following. The fast Fourier transform of a timeseries x(t) is X(f), the conjugated Fourier transform of a wavelet at a given scale ψσ(t) is 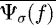, and the conjugate FFT of the transform components of a second variable y(t) is . The product of these three quantities is , which can be summed over f to give the wavelet coherence at scale σ, as shown in Supplementary Material, Appendix S2, equation (5). Alternatively we can then multiply this product by a vector of random phasors r(f) = eiϕ(f), as in box D, before summation to obtain a surrogate coherence value. This step is repeated as often as desired to obtain a distribution of surrogate coherences.

Where data is available from several locations to calculate a spatial coherence, a similarly efficient approach can be used to evaluate a surrogate spatial coherence (see Supplementary Material, Appendix S3).

thumbnail Fig. 3

Comparison of standard and efficient ways to calculate the wavelet coherence of a Fourier surrogate with some second variable. Multiple arrows are shown where the calculation must be performed for each timescale of the wavelet transform. Left (standard) algorithm: Box A is the procedure for generating a Fourier surrogate. Box B is the procedure for generating a wavelet transform of the surrogate (unscalloped). Box C is the procedure for calculating the wavelet coherence with the second variable. Most of the calculation time is taken up with Fourier transforms (coloured red). Boxes A, B and C are repeated every time a surrogate is generated. Right (fast) algorithm: Only the procedure in box D is repeated every time a surrogate is generated. The surrogate itself is defined by the random phases that are used, but is not constructed explicitly the way it was in box A.

2.4 Ecological data

The Continuous Plankton Recorder (CPR) survey carried out by the Sir Alister Hardy Foundation for Ocean Science monitors near-surface plankton in the North Sea, North Atlantic and elsewhere. The CPR sampling device is towed behind a ship. Organisms are caught on a silk ribbon fed between two rollers and their abundance quantified by manually counting individuals found in each 4 inch segment of silk, representing 10 nautical miles of tow, with subsampling for smaller organisms [22]. We examine time series from 1958 to 2010, inclusive, of annualized data based on CPR measurements, representing changes in the abundances of many individual plankton species, for 26 areas of the North Sea (see Supplementary Material, Appendix S4, Fig. S1). We include several Ceratium and dinoflagellate species as representatives of the phytoplankton, and a number of copepod species and groups which feed on the phytoplankton, plus the larvae of larger animal groups such as decapods (see Supplementary Material, Appendix S4, Tab. S1).

Using our accelerated approach, we compared the fluctuations in available ecological variables with each other and with those in relevant environmental variables. Our environmental timeseries are seasonal averages of sea surface temperature, wind speed (representing the tendency to mix the water), salinity (dependent on freshwater input from the coasts and saltier water from the ocean) and cloud cover (as a proxy for sunlight levels). Each was averaged over five different monthly ranges representing possibly relevant time periods in the annual bloom cycle of the plankton (see Supplementary Material, Appendix S4, Tab. S2).

2.5 Multiple-frequency testing

We determine an overall p-value for the wavelet coherence in a given frequency band using a procedure based on ranks, as described in Supplementary Material, Appendix S5. At each wavelet transform frequency we can find the rank of the actual coherence relative to all the surrogate coherences (i.e. the proportion of surrogates it exceeds). This gives a set of non-independent ranks, one for each frequency, which can be averaged to give an average rank for the frequency band. For comparison, we can consider each surrogate individually, compare it to the distribution of all the other surrogates, and find its mean rank for the band. The mean rank of a surrogate is expected to be close to 50%, with a spread that depends on the degree of non-independence of the coherence values in the band. The p-value is 1 minus the proportion of surrogate mean ranks exceeded by the actual mean rank, and is associated with the null hypothesis that the coherence throughout the whole band is not generally ranked higher relative to surrogates than would be expected by chance.

3 Results and discussion

The results of our efficient statistical tests on spatial wavelet coherence at low frequencies are shown in Figure 4. The results at high frequencies are shown in Figure 5. Coherence values not significant at the p < 0.05 level are masked with green, whereas significant values are indicated by a filled square with a colour indicating the phase shift between the variable indicated on the y axis and that on the x axis. The colour map is cyclic. Significance values are not Bonferroni corrected, so we expect a 5 percent false positive rate.

The low and high frequency coherence plots have several broad features in common. Physical variables of a given type (e.g. the different seasonal temperatures) all tend to be in phase with each other. Note how cloud cover and temperature variables tend to be in antiphase; sea surface temperature is lower in cloudier years.

The plankton species tend to be in phase with each other, with the Ceratium and dinoflagellate species largely coherent with each other. Zooplankton fluctuations show a more complicated pattern of significant in-phase relationships.

The results appear more stark at high than low frequencies, perhaps because there is more information available at high frequencies: more cycles of short-timescale fluctuations can fit into a time series of given length. Equivalently, in our methodology, the wavelet coherence is found to depend on a broader band of Fourier cross spectral values for shorter scales because the Fourier transform of the wavelet has a wider Gaussian profile. This gives additional statistical power (see Fig. 2b). Some zooplankton species and group fluctuations appear to be coherent with sea surface temperature fluctuations, such as Centropages typicus, Decapod larvae, and Calanus helgolandicus, which is known to be favoured by warmer water [23]. Several of the Ceratium phytoplankton species show a tendency to fluctuate in antiphase with Calanus finmarchicus and Calanus helgolandicus, which are major phytoplankton consumers.

Wavelet coherence and wavelet phase coherence approaches are optimal in slightly different circumstances; unfortunately, the significance of wavelet phase coherence cannot be tested using our efficient method. The wavelet coherence value is reflective of the tendency to maintain a phase relationship when and where amplitude is large, since small amplitude values make little contribution to the average that defines the wavelet coherence (Eq. (4)). The wavelet phase coherence (Eq. (1)) reflects the tendency to maintain a phase relationship irrespective of amplitude, which may be desirable if, e.g., large-amplitude fluctuations are associated with aberrant behavior or artefacts; or undesirable if, e.g., small-amplitude fluctuations are associated with poor signal to noise ratios. Because of the missing amplitude information, the Fourier transforms of the series eiϕ1,σ(t) and e−iϕ2,σ(t) (Eq. (3)) do not bear a straightforward relationship to the Fourier transforms of the time series from which they are derived, unlike w1,σ(t) and w2,σ(t) (Eq. (4)), so our fast algorithm cannot straightforwardly be adapted to wavelet phase coherence.

thumbnail Fig. 4

Phase shifts (ϕ) between wavelet transforms of environmental variables and plankton abundance fluctuations at low frequencies (σ > 4 years). Green squares represent non-significant spatial wavelet coherence values, as evaluated by our new efficient algorithm, other colours represent a significant (p < 0.05) phase relationship. We found p-values for all data comparisons using 10,000 spatial surrogates, and where p < 0.1 we repeated the test using 500,000 to obtain an accurate p-value.
thumbnail Fig. 5

Phase shifts (ϕ) between wavelet transforms of environmental variables and plankton abundance fluctuations at high frequencies (σ < 4 years). Green squares represent non-significant spatial wavelet coherence values, as evaluated by our new efficient algorithm, other colours represent a significant (p < 0.05) phase relationship. We found p-values for all data comparisons using 10,000 spatial surrogates, and where p < 0.1 we repeated the test using 500,000 to obtain an accurate p-value.

4 Conclusion

Wavelet coherence or spatial wavelet coherence of real or surrogate data can be rapidly calculated via our new method. For example, we have achieved a speed-up of over 600 times when testing 53 data points drawn from each of 26 locations (as used here). Precise speed-ups will depend on the data and the original implementation, but should only increase for more and longer timeseries. The methodology applied here is fast enough to be applied to testing large numbers of samples, large numbers of variables, and/or windowed or time localised wavelet coherence if desired. Efficient calculation of surrogate coherences also opens up the possibility of efficiently testing the goodness of fit of frequency-dependent wavelet models such as those developed to explain spatial synchrony in biological fluctuations [8].

Via our new method, coherence (Eq. (4)) or spatial coherence (Eq. (5)) is ultimately a sum of products in the frequency domain (see Supplementary Material, Appendix S2). Examination of the products provides a new way of understanding the standard result that coherence is biased towards high magnitude for little data and long timescales. Only a few Fourier frequency components have large magnitude for any given wavelet scale. The shorter the original timeseries the fewer Fourier components fall in a given frequency band. The longer the scale, the narrower the wavelet filter, resulting in a large contribution from only a few components. Each component has random phase, but the magnitude of the sum of a few large random components is systematically greater than that of many small ones.

Understanding and computing the expectation value of the coherence under the null hypothesis gives us confidence in the phase relationships that are found. In the complex biophysical system represented by plankton ecology in the North Sea, we find a general tendency for in-phase fluctuations in abundance between plankton species, complicated by idiosyncratic relationships between certain species and between species abundances and physical variables. Where significant, the frequency-dependent phase relationships between biophysical variables may illuminate the complex interactions that underpin their dynamics.

Conflicts of interest

The authors declare that they have no conflicts of interest in relation to this article.

Supplementary Material

Appendix S1 The Morlet wavelet transform.

Appendix S2 Details of method.

Appendix S3 Efficient testing of spatial coherence.

Appendix S4 Data.

Appendix S5 Multiple-frequency testing.

MATLAB code

Access here

Acknowledgments

We thank Joel E. Cohen, Robert Desharnais and the BRACCIA team for helpful discussions. LWS and DCR were partly supported by United Kingdom Natural Environment Research Council grants NE/H020705/1, NE/I010963/1, and NE/I011889/1, University of Kansas tier II and General Research Fund grants, the James S McDonnell Foundation, and United States National Science Foundation grant 1442595.

References

  1. L.W. Sheppard, A. Stefanovska, P.V.E. McClintock, Testing for time-localized coherence in bivariate data, Phys. Rev. E 85, 046205 (2012) [CrossRef] [Google Scholar]
  2. L.W. Sheppard, V. Vuksanovi, P.V.E. McClintock, A. Stefanovska, Oscillatory dynamics of vasoconstriction and vasodilation identified by time-localized phase coherence, Phys. Med. Biol. 56, 3583 (2011) [CrossRef] [Google Scholar]
  3. D.A. Kenwright, A. Bernjak, T. Draegni, S. Dzeroski, M. Entwistle, M. Horvat, P. Kvandal, S.A. Landsverk, P.V.E. McClintock, B. Musizza, J. Petrovi, J. Raeder, L.W. Sheppard, A.F. Smith, T. Stankovski, A. Stefanovska, The discriminatory value of cardiorespiratory interactions in distinguishing awake from anaesthetised states: a randomised observational study, Anaesthesia 70, 1356 (2015) [CrossRef] [Google Scholar]
  4. P. Kvandal, L.W. Sheppard, S.A. Landsverk, A. Stefanovska, K.A. Kirkeboen, Impaired cerebrovascular reactivity after acute traumatic brain injury can be detected by wavelet phase coherence analysis of the intracranial and arterial blood pressure signals, J. Clin. Monitor. Comput. 27, 375 (2013) [CrossRef] [Google Scholar]
  5. B.T. Grenfell, O.N. Bjørnstad, J. Kappey, Travelling waves and spatial hierarchies in measles epidemics, Nature 414, 716 (2001) [CrossRef] [PubMed] [Google Scholar]
  6. T.H. Keitt, Coherent ecological dynamics induced by large-scale disturbance, Nature 454, 331 (2008) [CrossRef] [Google Scholar]
  7. T.H. Keitt, J. Fischer, Detection of scale-specific community dynamics using wavelets, Ecology 87, 2895 (2006) [CrossRef] [Google Scholar]
  8. L.W. Sheppard, J.R. Bell, R. Harrington, D.C. Reuman, Changes in large-scale climate alter spatial synchrony of aphid pests, Nat. Clim. Change 6, 610 (2016) [CrossRef] [Google Scholar]
  9. C. Viboud, O.N. Bjørnstad, D.L. Smith, L. Simonsen, M.A. Miller, B.T. Grenfell, Synchrony, waves, and spatial hierarchies in the spread of influenza, Science 312, 447 (2006) [CrossRef] [PubMed] [Google Scholar]
  10. J.M. Colebrook, Sea surface temperature and zooplankton, North Sea, 1948 to 1983, ICES J. 42, 179 (1985) [CrossRef] [Google Scholar]
  11. A. Bandrivskyy, A. Bernjak, P.V.E. McClintock, A. Stefanovska, Wavelet phase coherence analysis: application to skin temperature and blood flow, Cardiovasc. Eng. 4, 89 (2004) [CrossRef] [Google Scholar]
  12. N.I. Fisher, Statistical analysis of circular data (Cambridge University Press, Cambridge, 1993) [CrossRef] [Google Scholar]
  13. T. Schreiber, A. Schmitz, Surrogate time series, Physica D 142, 346 (2000) [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. J. Theiler, S. Eubank, A. Longtin, B. Galdrikian, J.D. Farmer, Testing for nonlinearity in time series: the method of surrogate data, Physica D 58, 77 (1992) [NASA ADS] [CrossRef] [Google Scholar]
  15. D. Prichard, J. Theiler, Generating surrogate data for time series with several simultaneously measured variables, Phys. Rev. Lett. 73, 951 (1994) [NASA ADS] [CrossRef] [Google Scholar]
  16. D.R. Brillinger, Time series: data analysis and theory (Holt, Rinehart and Winston, New York, 1975) [Google Scholar]
  17. A. Pikovsky, M. Rosenblum, J. Kurths, Synchronization – a universal concept in nonlinear sciences (Cambridge University Press, Cambridge, 2001) [CrossRef] [Google Scholar]
  18. A. Stefanovska, Coupled oscillators: complex but not complicated cardiovascular and brain interactions, IEEE Eng. Med. Biol. Mag. 26, 25 (2007) [CrossRef] [Google Scholar]
  19. P.S. Addison, The illustrated wavelet transform handbook: introductory theory and applications in science, engineering, medicine and finance (Taylor and Francis, New York, 2002) [Google Scholar]
  20. C. Torrence, G.P. Compo, A practical guide to wavelet analysis, Bull. Am. Meteorol. Soc. 79, 61 (1998) [Google Scholar]
  21. B.B. Percival, A.T. Walden, Wavelet methods for time series analysis (Cambridge University Press, Cambridge, 2000) [Google Scholar]
  22. J.M. Colebrook, G.A. Robinson, Continuous plankton records: seasonal cycles of phytoplankton and copepods in the North-Eastern Atlantic and the North Sea, Bull. Mar. Ecol. 6, 123 (1965) [Google Scholar]
  23. J. Lindley, P. Reid, Variations in the abundance of Centropages typicus and Calanus helgolandicus in the North Sea: deviations from close relationships with temperature, Mar. Biol. 141, 153 (2002) [CrossRef] [Google Scholar]

Cite this article as: Lawrence W. Sheppard, Philip C. Reid, Daniel C. Reuman, Rapid surrogate testing of wavelet coherences, EPJ Nonlinear Biomed. Phys. 5, 1 (2017)

All Figures

thumbnail Fig. 1

(a) Phase shift of wavelet components of the first difference of h(t) relative to h(t), in blue, and phase shift of wavelet components of the cumulative sum of h(t) relative to h(t), in red. Black lines are at π/2 and −π/2. (b) The driver, h(t), is white noise, with a power spectrum shown in green (the area under the curve represents the wavelet power in a spectral interval), while the power spectrum of the first difference of h(t) is shown in blue and that of the cumulative sum is in red.
In the text
thumbnail Fig. 2

The false positive rate obtained at each frequency for tests of wavelet coherence based on independent data (a); and the false negative rate for an example of partly correlated data (b). The standard wavelet coherence algorithm is in red; the new, fast algorithm using circular convolutions and no scalloping is in green. Rates are based on 1000 simulations. Tests are based on 1000 surrogate data sets for each. See text for additional details.
In the text
thumbnail Fig. 3

Comparison of standard and efficient ways to calculate the wavelet coherence of a Fourier surrogate with some second variable. Multiple arrows are shown where the calculation must be performed for each timescale of the wavelet transform. Left (standard) algorithm: Box A is the procedure for generating a Fourier surrogate. Box B is the procedure for generating a wavelet transform of the surrogate (unscalloped). Box C is the procedure for calculating the wavelet coherence with the second variable. Most of the calculation time is taken up with Fourier transforms (coloured red). Boxes A, B and C are repeated every time a surrogate is generated. Right (fast) algorithm: Only the procedure in box D is repeated every time a surrogate is generated. The surrogate itself is defined by the random phases that are used, but is not constructed explicitly the way it was in box A.
In the text
thumbnail Fig. 4

Phase shifts (ϕ) between wavelet transforms of environmental variables and plankton abundance fluctuations at low frequencies (σ > 4 years). Green squares represent non-significant spatial wavelet coherence values, as evaluated by our new efficient algorithm, other colours represent a significant (p < 0.05) phase relationship. We found p-values for all data comparisons using 10,000 spatial surrogates, and where p < 0.1 we repeated the test using 500,000 to obtain an accurate p-value.
In the text
thumbnail Fig. 5

Phase shifts (ϕ) between wavelet transforms of environmental variables and plankton abundance fluctuations at high frequencies (σ < 4 years). Green squares represent non-significant spatial wavelet coherence values, as evaluated by our new efficient algorithm, other colours represent a significant (p < 0.05) phase relationship. We found p-values for all data comparisons using 10,000 spatial surrogates, and where p < 0.1 we repeated the test using 500,000 to obtain an accurate p-value.
In the text