Search
Menu
All issues Volume 5 (2017) EPJ Nonlinear Biomed. Phys., 5 (2017) 3 Full HTML
Open Access
Issue
EPJ Nonlinear Biomed. Phys.
Volume 5, 2017
Article Number 3
Number of page(s) 11
Section Physics of Biological Systems and Their Interactions
DOI https://doi.org/10.1051/epjnbp/2017002
Published online 07 September 2017

© K. Schiecke et al., published by EDP Sciences, 2017

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Background

The detection and quantification of directed (causal) interactions within the brain and their time courses are of highest interest in neuroscience in general and in particular for the investigation of epilepsy. Temporal lobe epilepsy (TLE) is the most common medically intractable epilepsy in adults, which is frequently associated with mesial hippocampal sclerosis (mesial TLE), characterized by severe neuronal cell loss and change of glial cells in the hippocampus. The zone concept of epileptic seizure generation implies that the hippocampus and other areas of the temporal cortex can act as epileptic focus for seizure-onset generation (focal onset), from which the seizure spread via a preferred pathway to cortical and subcortical brain regions. This traditional concept has been falsified by many experimental and clinical results and can be seen as an overschematized simplification [1]. An important clinical point is whether or not the clinical symptomatology is stereotyped: stereotype favors focal onset. Particularly in cases with frequently occurring seizures, the stereotypy can break down, i.e. for subsequent seizures the onset-triggering brain area can change from seizure to seizure. However, the mesial TLE (mTLE) seizure is most probably preceded by a state of enhanced excitability [2].

Additionally, the paths for seizure propagation can also change dynamically, i.e. different spatiotemporal propagation patterns occur. These insights were obtained by using implanted depth electrodes. The underlying coordinated neuronal mass activities span functionally diverse and structurally widely distributed cortical and subcortical brain regions, i.e. a dynamic, distributed epileptic network can be assumed. Consequently, connectivity and synchronization analysis could be helpful to understand the processes that contribute to the seizure onset and propagation (for example see [3,4]). Such research objectives are related to functional and effective network analysis. The investigation of the functional connectivity, which quantifies the statistical dependencies between neurophysiological signals, “helps to elucidate how a structural architecture gives rise to alterations in neurophysiological dynamics” [5]. Furthermore, “one wishes to estimate causal relations within the set of EEG signals that belong to the epileptic network” [2].

Of high importance is the practical question whether the EEG is appropriate to provide information concerning the functional and/or effective network connectivity before, during, and after the seizure. Its high time-resolution can be seen as a big advantage. Lopes da Silva [2] proposed three possible ways by which changes of excitability state of neural networks before, during, and after the mTLE seizure might be detected: (1) analysis of spontaneous EEG signals, (2) detection and analysis of EEG markers (e.g. high-frequency ripples), and (3) recording of activity evoked by electrical stimulation via implanted electrodes.

The assumed dynamic causal relations can be investigated by effective connectivity measures, which provide the directionality of the relation [6]. Different measures exist to define those directed interaction, and the most popular are based on the concept of the Granger causality (GC) [7]. GC uses the driver data X to predict the response data Y (forward method) and is linear in most of its implementation. Multivariate generalizations exist [8]; partial directed coherence (PDC) allows time-variant and frequency-selective investigations [6]. A review of methods for the determination of directed connectivity based on multivariate autoregressive (MVAR) models can be found in [9]. The transfer entropy (TE) [10,11] is a model-free measure of information transfer and is able to generalize GC to the detection of many different types of linear and nonlinear interactions in multivariate time series [9]. Time-variant investigations by means of TE are afflicted with the problem of data length needed for estimation; for the efficiency of TE in analyzing nonstationary data see [12].

In contrast, convergent cross mapping (CCM), introduced by Sugihara et al. [13], defines nonlinear interactions between time series in terms of nonlinear stability. CCM looks at the correspondence between so-called “shadow manifolds” constructed from lagged coordinates by nonlinear state space reconstruction of the time series values of X and Y. Thus, CCM uses the historical record of values of response Y to estimate values of the driver X. CCM is bivariate and time-invariant in its original implementation [13]. Application of CCM can be found mostly in the field of ecology, biology, and geoscience (e.g. [14,15]).

In [16] we provided an advanced time-variant investigation of CCM to analyze interaction between the heart rate variability (HRV) and specific EEG components of the same group children with TLE. We could prove that AR-based gPDC analysis failed for our data, mainly due to the fact that our data seems to not fit in the concept of (linear) AR-modeling. On the other hand, by applying CCM we could show that statistical significant directed nonlinear interactions between specific components of the EEG (in the range of δ-activity and α-activity) and the HRV exists in the preictal, ictal and postictal periods of children with TLE. Our investigation revealed distinct time courses of such directed interactions. A consequent logical step for the deeper understanding of the functioning of the epileptic neural network is to extend this investigation to an examination of interactions within the EEG activity and specific components of EEG activity (δ-activity and α-activity) following the same methodological concept of applying time-variant multivariate linear AR-modeling and time-variant bivariate nonlinear CCM analysis.

2 Subjects and data material

We investigated the EEG recordings of 18 children with TLE obtained during presurgical evaluation performed at the Vienna pediatric epilepsy center following a standard protocol. The protocol was approved by the local ethical committee of the University Hospital Vienna. For each patient, EEG (23 channels; 20 channels were used for our investigations) was recorded referentially from gold disk electrodes placed according to the extended 10–20 system with additional temporal electrodes. EEG data were recorded referentially against electrode position CPZ, filtered (1–70 Hz), converted from analog to digital (sampling frequency 256 Hz, 12 bit), and stored digitally for further data analysis. Further information concerning the classification of seizure type, onset, and termination can be found in [17,18]. One recording per patient was analyzed containing 5 min before (preictal period) and 5 min after the seizure onset (ictal and postictal periods).

After downsampling the EEG data from 256 Hz to 64 Hz, an artifact removal procedure was applied, using the independent component analysis (ICA) provided by the FieldTrip toolbox [19]. For each child, the EEG signals were decomposed with ICA and the resulting components were visually inspected. The independent components (ICs) most affected by ocular or movement artifacts were removed and the signals were reconstructed using the remaining ICs. A detailed description of results of ICA decomposition of epileptic EEG can be found in [20]. That was followed by re-referencing of the EEG to the average reference montage. Finally, 20 channels of EEG were selected for further analysis.

3 Methods

The general design of the processing scheme is depicted in Figure 1. Investigated data, preprocessing, and main characteristics of adapted approaches are given. Details about all applied methods will be given in the following sections.

thumbnail Fig. 1

General design of processing scheme. Investigated data, preprocessing, and the main characteristics of the applied approaches as well as statistical measures are given.

3.1 Linear multivariate autoregressive (MVAR) models

MVAR models were fitted to each child separately. For N time series X = (X1, …, XN) (in our case, N EEG channels), the MVAR model is given by 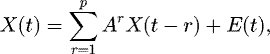(1) where p denotes the order of the model and E(t) represents the model residuals. The matrices Ar contain the model parameters; thus, the (i, j)th entry 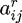provides the coefficient that weights the modeled contribution of the jth time series to the modeled ith time series at time point t − r. Due to the considerably differing data properties among preictal, ictal, and postictal periods, a temporally varying model is required; that means, the parameter matrices Ar have to be dependent on the sampling point t: (2)

To realize this, time-variant model parameters were estimated by means of the general linear Kalman filter [8]. The model order p was chosen according to Akaike's information criterion (p = 10).

3.2 Multivariate empirical mode decomposition (MEMD)

Multivariate empirical mode decomposition (MEMD) was introduced by Rehman and Mandic [21] as a multivariate extension of the standard EMD. The advantage of EMD is that this is a signal-adaptive algorithm for multiscale decomposition and time–frequency analysis of multicomponent signals [22] preserving the nonlinearity of data. EMD decomposes the multicomponent signal into a finite number of amplitude and frequency-modulated zero mean oscillatory signals [23], called intrinsic mode functions (IMFs), and a monotonic residual. MEMD calculates the IMFs for all channels at the same time. Therefore, MEMD has the advantage of resulting in the same number of IMFs for all investigated channels, whereas EMD computation of the IMFs for the single channels results in a different number of IMFs for each EEG channel. This would lead to the correspondence problem, when a certain frequency band component has to be selected for further analysis. Using MEMD, for each child, the same number of IMFs is obtained for all channels. However, the number of IMFs might differ between children. Thus, for group analysis, consideration of power spectra is a standard method to investigate the properties of specific IMFs [24,25] and to select IMFs of interest.

3.3 Convergent cross mapping (CCM)

Basic idea of CCM is to test for causation between time series X and Y by looking at the correspondence between so-called shadow manifolds constructed from lagged coordinates of the time series values of X and Y. Contrary to intuition and particularly the concept of GC, the causality concept of CCM is that when causation is unilateral (“X drives Y”), then it is possible to estimate X from Y, but not Y from X. CCM correlation defined by the absolute value of the Pearson correlation coefficient between the original time series X and an estimation of X using the CCM with Y quantifies interaction from time series X to Y (and the one between the original time series Y and an estimation of Y using the CCM with X quantifies interactions from Y to X, respectively): (3)

For any pair of time series X and Y, both values CCMX→Y and CCMY→X are compared to determine the bivariate CCM. Practically, CCMX→Y and CCMY→X are examined using data sets X = x(t) and Y = x(t) of increasing data length L (the so-called “library length”). Information about the basic algorithm for cross mapping of X by using MY (CCMX→Y) for each library length L (and CCMY→X respectively) can be found in [16] and in the supplementary material of [13]. The following are the main steps:

  • generate “shadow manifold” MY;

  • find defined number of nearest neighbors at each time point t in MY;

  • generate weight matrix by use of nearest neighbors;

  • estimate by use of these weights;

  • calculate correlation coefficient ρ (or other error metric) between x(t) and .

Estimation is performed accordingly for cross mapping of Y by using MX (CCMY→X).

In the bidirectional case “X drives Y stronger than vice versa,” CCMX→Y converges faster and reaches a higher plateau than CCMY→X. Additionally, to also be able to investigate time-varying directed interactions between time series X and Y, an interval-based estimation can be performed by using a sliding window of an appropriate library length L.

Clearly the performance of the CCM estimation depends on estimation parameters such as embedding dimension, time lag, library length, as well as used error metrics. Furthermore, system noise is strongly influencing the estimation of CCM. Simulations concerning those influences were performed in [16].

3.4 Statistical evaluation

The statistical testing for CCM was performed using (i) a surrogate data approach to find a threshold to quantify statistical significant interactions in dependence on the used library length L and (ii) a bootstrapping approach to quantify statistical properties of single CCM courses estimated for K (K = 18) realizations of the investigated data.

The null hypothesis of the surrogate data approach is that there is no interaction between time series X and Y (“small values of CCM”). Surrogate data were obtained by destroying the phase information of investigated signals by means of phase randomization [26] destroying the Fourier phases but remaining the power spectra of the signals. For each investigation, 50 surrogate data sets per realization (K = 18 children) were obtained resulting in 900 repetitions per situation. CCM estimations were carried out for increasing library length (L = 128, 256, …, 2560 data points). The 95th percentile of the surrogate data's CCM was computed for each library length L and serves as the library length dependent threshold for statistically significant CCM values (see e.g. [27]).

Aim of the bootstrapping approach is to determine statistical properties of CCM estimated for K = 18 realizations of each investigated data set. Here, statistical properties of CCM values in dependence of increasing library length L and of CCM values achieved by time-varying interval-based approach are of interest. In order to estimate confidence tubes of the extracted CCM courses without any particular distribution assumption, 1000 bootstrap samples of size K = 18 were drawn from the estimated CCM (courses of increasing library length or time courses achieved by interval-based approach, accordingly) by a case resampling with replacement. With it, 1000 bootstrap replications of each extracted parameter were computed. Based on these replications, the lower limit (the 2.5% quantile) defined the lower bound, and the upper limit (the 97.5% quantile) defined the upper bound of the 95% confidence tube of CCM. For theoretical details concerning bootstrapping approaches see [28].

3.5 Protocol of analyses

After recording and preprocessing of data, MVAR modeling was performed for the 20 EEG channels (N = 20 in the multivariate approach) for all children and compared to a univariate AR model approach. Furthermore, MEMD [21] was performed for each child preserving the nonlinearity of data and resulting in so-called IMFs. Time-invariant spectra of all IMFs were computed with the Fourier transform over 10 min epochs per channel. Distribution of the frequency characteristic was used to quantify the frequency range of IMFs by estimating the median as well as the 25th and 75th percentile of frequencies of the IMFs of each channel and each child. The two IMFs that have the frequency characteristics most related to the delta band EEG activity (δ-EEG) and to the alpha band EEG activity (α-EEG) were selected for further analysis.

Bivariate CCM analyses of EEG activity, δ-EEG-activity, and α-EEG-activity between specific electrode locations which are of most interest for TLE, were performed for all children. An example of original data of one child (focus of seizure at left side) is given in Figure 2. For nonlinear state space reconstruction, an embedding dimension of D = 8 and a time lag τ = 5 were used [17]. Increasing library lengths L of 128 samples (2 s) to 2560 samples (40 s) were investigated using the data of preictal period (period of 200–240 s was analyzed), and L = 256 samples (4 s) were used for interval-based analysis of the whole recording (10 min; preictal, ictal, and postictal periods; sliding windows).

A schematic overview of investigated CCM is given in Figure 3. The color code of investigated interactions between specific electrode positions of interest in Figure 3 is adapted to the result section. The following nonlinear interactions, separately for the EEG, the δ-EEG, and the α-EEG, were investigated:

  • “ipsilateral vs. contralateral”: T3 vs. T4 for children with left side seizure (N = 9), T4 vs. T3 for children with right side seizure (N = 9);

  • “ipsilateral nearby”: T3 vs. C3 for children with left side seizure (N = 9), T4 vs. C4 for children with right side seizure (N = 9);

  • “ipsilateral far away”: T3 vs. Fp1 for children with left side seizure (N = 9), T4 vs. Fp2 for children with right side seizure (N = 9).

thumbnail Fig. 2

Time courses of original data and extracted EEG components of one child (left side focus). Investigated electrode positions and focus of seizure are given in (A); example of original EEG recording at ipsilateral focus area electrode (blue), contralateral focus area electrode (red), ipsilateral near to focus area electrode (green), as well as ipsilateral far away from focus area electrode (cyan) are given in (B), and extracted δ- and α-IMFs are shown in (C). Black bold line designates onset of seizure at 5 min.
thumbnail Fig. 3

Schematic overview of investigated CCMs. Interactions within EEG activity, within δ-EEG activity, as well as within α-EEG activity are examined at (A) ipsilateral vs. contralateral focus area positions, (B) ipsilateral near to focus area positions, and (C) ipsilateral far away from focus area positions for all children. Electrode positions are given for left-sided focus (note different locations for right-sided seizures in brackets).

4 Results

4.1 Linear AR-modeling

As a general result, it can be noticed that MVAR models seem to be inappropriate for our data. The reason is that the diagonal entries of the parameter matrices Ar are by far higher than the off-diagonal entries (see Figs. 4A–4C, relevant time points of the preictal, ictal, and postictal periods are shown for one child). In other words, for each time point of one channel, the most prominent model parameter is that coefficient, which corresponds to the past of this channel (“each channel is modeled best my itself”). Consequently, the multivariate approach should not have any advantage to the univariate approach, which solely includes one channel, neglecting the information of all other recorded time series. Comparisons of estimated univariate and multivariate approaches are shown in Figures 4D and 4E (example of estimated time series of electrodes T3 and T4 for one child) and verify the finding that the multivariate approach does not have any advantage to the univariate approach. Accordingly, any subsequent application of linear AR-based connectivity measures such as GC or PDC is not meaningful for our specific data.

thumbnail Fig. 4

MVAR results of one child. Multivariate AR parameter matrices during preictal (A), ictal (B), and postictal periods (C) are shown, illustrating the dominance of all diagonal entries. Furthermore, estimated time series of electrodes T3 (D) and T4 (E) are depicted, where the blue line represents the use of univariate estimation (only one channel is used) and the gray line depicts the use of multivariate estimation (all channels are included to the model). Specific time points of MVAR parameter shown in (A) to (C) are marked in (D) and (E) by dashed red lines.

4.2 Nonlinear CCM analysis

Results of investigations of bivariate CCM are given in Figures 5–8. Color code of Figures 6–8 is adapted from Figure 3.

Investigation of increasing library length L (Fig. 5, only the investigation of EEG activity is shown) and applied bootstrapping approach did not reveal statistically different CCMs between the three different electrode locations (A–C in Fig. 5) or statistically different CCM values concerning the directionality (upper and lower rows in Fig. 5). However, applied surrogate data approach provided statistical threshold for significant CCM values (bold lines in each subplot of Fig. 5) and thus the appropriate library length of L = 4 s (vertical thin line in each subplot of Fig. 5).

The time courses of interval-based CCM analyses at “ipsilateral vs. contralateral” locations (Fig. 6) reveal highest interactions in the δ-EEG (blue line) and lowest in the α-EEG band (red line) during the preictal period. With seizure onset, CCM of EEG clearly increases (black line). The increase of CCM in the δ-EEG is less pronounced. Both remain increased in the postictal period. CCM in the α-EEG slightly increases with seizure but clearly decreases in the postictal period. Again, no differences in the directionality of interactions (blue/black/red line in Fig. 6A vs. cyan/gray/magenta line in Fig. 6B) could be shown possibly revealing the generalized character of such a seizure.

Therefore, the comparison of all three investigated electrode locations is shown only for one direction of CCM (A–C in Fig. 7). Figure 7 replicates the results of Figure 6 for EEG activity (black line) and δ-EEG activity (blue line) interactions. The main difference is that modified interactions occur in the α-EEG activity (red line). For both, the nearby location (Fig. 7B) and far away location (Fig. 7C), CCM is lower during preictal period, for nearby location, CCM only slightly increases during ictal period (and no increase could be shown for the far away location), and for both locations CCM does not drop in the postictal period.

Statistical evaluations of all CCM results are given in Figure 8. Results of all investigated locations (Figs. 8A–8C) and for EEG, δ-EEG, and α-EEG interactions (upper to lower rows in Fig. 8) are shown.

Confidence tubes achieved by bootstrapping revealed statistical significant differences between preictal and postictal periods within the EEG (black line) and δ-EEG (blue line) interactions and also between EEG (black line) and δ-EEG (blue line) interactions during preictal and ictal periods for all three investigated locations (nonoverlapping tubes in Figs. 8A–8C). There is no significant difference between preictal and postictal periods within the α-EEG (red line) interactions for all three locations, but significant difference was observed between α-EEG (red line) and δ-EEG (blue line) during all periods and between α-EEG (red line) and EEG (black line) during ictal and postictal periods. Furthermore, clear differences in the variance of CCM estimation are visible in the broadness of confidence tubes, especially by comparing not only the one of EEG activity (black) and specific components of EEG activity (blue and red), but also by comparing estimation during preictal, ictal, and postictal periods for the EEG activity; much broader confidence tubes could be found during the preictal period, most possibly due to interindividual differences.

Surrogate data approach provided thresholds for statistically significant CCM values (blue, black and red thin lines in all subplots of Fig. 8). Significant CCM values could be proven for the investigation of EEG and δ-EEG interactions (black and blue lines) for all three investigated locations (lines does not cover confidence tubes in Figs. 8A–8C), for the investigation of α-EEG (red line), significant CCM values could be found only in the preictal and ictal periods of the interaction “ipsilateral vs. contralateral” (Fig. 8A).

thumbnail Fig. 5

Results of the investigation of increasing library length L on the estimation of CCM. Mean results of all children (K = 18) are shown. CCM and tubes of 95% CI of bootstrapping approach, bold lines designating the statistical thresholds by surrogate data approach, as well as appropriate library length of L = 4 s (vertical thin line) are shown.
thumbnail Fig. 6

Results of time-varying interval-based investigation of CCM of the ipsilateral vs. contralateral focus area. A sliding window of 4 s (=256 data points) is used. In (A) and (B), both directions of interval-based results of CCM of EEG activity (black and gray), δ-EEG activity (blue and cyan), as well as α-EEG activity (red and magenta) are shown (mean result of all children; color code of direction according to Fig. 3). Gray rectangle marks onset and median length of seizure.
thumbnail Fig. 7

Results of time-varying interval-based investigation of CCM in dependence to the investigated electrode positions. Only one direction of interaction is shown (ipsilateral focus area to other positions). In (A) to (C), interval-based results of CCM of EEG activity (black), δ-EEG activity (blue), as well as α-EEG activity (red) are shown for all three different investigated electrode positions (mean result of all children; color code according to Fig. 3). Gray rectangle marks onset and median length of seizure.
thumbnail Fig. 8

Results of statistical evaluation of time-varying interval-based investigation of CCM in dependence to the investigated electrode positions. Only one direction of interaction is shown (ipsilateral focus area to other positions). In (A) to (C), interval-based results of CCM of EEG activity (black), δ-EEG activity (blue), as well as α-EEG activity (red) are shown for all investigated electrode positions (mean result of all children). Confidence tubes achieved by bootstrapping and statistical threshold for significant CCM values (thin lines) are given according to the color code (Fig. 3). Gray rectangle marks onset and median length of seizure.

5 Discussion and conclusions

There are only a few of studies using the time-variant MVAR-based connectivity measures to reveal the interactions between brain areas during epilepsy. The first pilot studies were carried out by Franaszczuk and Bergey [29] who used DTF for the analysis of the seizure activity (e.g. from mesial temporal structures) derived from subdural and implanted depth electrodes. DTF was also used for studying MEG-based source connectivity during interictal discharges [30]. The study of Wilke et al. [31] is based on the ECoG and analyzed the interictal discharges. Furthermore, other measures were used to investigate the connectivity, e.g. nonlinear connectivity in patients with mTLE (Bettus et al. [32], nonlinear correlation, implanted depth electrodes) and cross-frequency analysis (Villa and Tetko [33], foramen oval electrodes). A review concerning connectivity analysis of epileptic networks was given by Stefan and Lopes da Silva [34]. This overview demonstrates that novel analysis methods can provide new insights concerning connectivity between more (whole head recordings) or less remote (implanted electrodes) brain areas.

In general, the advanced CCM method we applied provides the possibility to investigate nonlinear and time-variant directed interactions between time-series but is inflicted with the limitation of a bivariate implementation. Linear GC-based measures such as AR-based gPDC are time-variant and multivariate, and often also work in the presence of nonlinearity (for example see [35], comprehensive comparison of CCM and GC in the supplement of [13]). Because a time-varying investigation of TE is not trivial [12], TE was not adapted in our current study but should be investigated for these data in the future.

In a former study [16], we have shown that CCM is able to replicate defined directed interactions in simulated deterministic system and systems with a certain level of additive noise. The introduced moving window-based time-varying implementation of CCM is able to replicate correct directionality and (relative) strength of interactions also by using rather short window lengths. From the statistical point a view, surrogate data tests provide window-length dependent thresholds for the statistical significance of such interactions. We adapted the approach of Theiler et al. [26] to our data. To focus more on the comparison between linear and nonlinear methods the approach of Prichard and Theiler [36] should be applied providing surrogates that destroy the Fourier phases in the two signals but preserve their difference in terms of linear autocorrelations and cross-correlations.

In our current analysis of interactions within EEG activity, the performed downsampling of EEG recordings to 64 Hz may raise questions. Epileptic activity has also very high frequency components. This has to taken into account for the discussion of CCM interaction of the pure EEG activity but not for the two specific IMFs (δ- and α-activities), which are not inflicted by the cutoff frequency. Furthermore EEG signals are usually affected by volume conduction, which induces correlated sensor activities at neighboring sensors by superposition of underlying brain source activities, leading to misinterpretations of obtained interaction results [37]. For the epilepsy monitoring of children with TLE, the recording of surface EEG rather than depth electrodes as well as the rather lower number of available recording sites is a typical clinical setting preventing a meaningful source modeling. Besides, we should have in mind that re-referencing are crucial in scalp-based EEG connectivity analyses [38], and that the preprocessing steps (in our case: ICA, MEMD), even if they preserve the nonlinearity of signals (MEMD), may alter the phase relations between signals and thus affect connectivity estimates.

By analyzing interactions within the EEG activity of children during TLE, we could prove that MVAR-modeling failed for these specific data. This is possibly due to the fact that these data seem to not fit in the linear concept of MVAR-modeling; we could show that there is no advantage of MVAR to a univariate AR-modeling, and each channel is modeled best by itself. For this finding, different possible explanations exist. Firstly, there are no interactions at all. That would be very uncommon in case of epileptic data. Secondly, either interactions are fully nonlinear or we do have a mixture of linear and strong nonlinear interactions. MVAR models are linear and can provide only local linear approximations. Nevertheless, from the practical point of view, MVAR models are able to quantify nonlinear interactions to a certain extent [35,39]. The concrete practical results of MVAR-modeling depend on the degree of nonlinearity and surely can be erroneous. Theoretically, MVAR models should work but require a sufficiently long enough data set and an adequately high AR-order [39] practically not being adaptable for the time-variant analysis of epileptic seizure activity. But still there is the question why we do have the observation of essentially diagonal and very small values at all nondiagonal coefficient matrices. Thirdly, the possible best explanation is that we know that connectivity analyses based on time-variant MVAR-modeling are very sensitive to additive noise [6]. Additive white noise decreases all coefficient matrices of our MVAR model to zero. More general, an additive superposition of any uncoupled process would result in a decrease of nondiagonal coefficient matrices. Therefore, fourthly, in addition to noise, other uncoupled artifacts may influence the results of MVAR-modeling in a manner as observed in our data.

By applying CCM, we have shown that statistically significant nonlinear interactions within the EEG activity as well as within specific components of the EEG (stronger not only in the range of δ-activity but also in the range of α-activity) exist in the preictal, ictal, and postictal periods. Our investigation revealed distinct time courses of such interactions. Particularly the dissimilarities of time pattern of interactions occurring in the different components of EEG activity we investigated (δ-activity vs. α-activity) uncovered the high complexity of the underlying processes. No distinct results could be found concerning the presumed directionalities of interaction, especially with regard to the known focus location of seizure. By analyzing strength and direction of interactions within EEG recordings, Lehnertz and Dickten [40] argued that it remains unclear whether the dynamic of seizure-onset zone “indeed be characterized by an elevated local synchrony or elevated strength of interactions” and thus also guided the discussion to a more general view of “epileptic network” rather than “epileptic focus.” Physiological networks are of great interest in many fields of neuroscience [41–43]. Our results contribute to the development of the field of network physiology [44] as well as nonlinear directed interactions. Seizure prediction being another major clinical objective for epileptic patients was not the focus of our investigation.

In summary, the advantage of CCM is to uncover time pattern of nonlinear interactions thereby possibly contributing to the further understanding of complex behavior of the brain during TLE. Our investigation of nonlinear CCM may provide deeper insight into physiological state of complex networks, e.g. during the development of an epileptic seizure or the recovery in the postictal state. From the methodological point of view, we have to take in account the disadvantage of the bivariate implementation of CCM. Comparison to TE or other nonlinear and/or model-free approaches should follow.

Authors' contributions

KS, HW, and LL conceived and designed the study. MF and FB conceived the clinical standard protocol and recorded the data. KS, BP, and DP preprocessed and analyzed the data. KS, HW, and LL drafted the manuscript. All authors read and approved the final manuscript.

Conflicts of interest

The authors declare that they have no conflicts of interest in relation to this article.

Acknowledgments

This work was supported by the DFG grant Wi 1166/12-2 Le 2025/6-2.

References

  1. S.A. Chkhenkeli, M. Sramka, T.N. Rakviashvili, G.S. Lortkipanidze, G.E. Magalashvili, E. Bregvadze et al., Bitemporal intractable epilepsy: could it be surgically treatable? Stereotact. Funct. Neurosurg. 91, 104 (2013) [CrossRef] [Google Scholar]
  2. F.H. Lopes da Silva, Epilepsy as a dynamic disease of neuronal networks, in Epilepsy: Basic Principles and Diagnosis. Handbook of Clinical Neurology, edited by H. Stefan, W. Theodore (Elsevier, Amsterdam, 2012), pp. 35–62 [CrossRef] [Google Scholar]
  3. R.T. Constable, D. Scheinost, E.S. Finn, X. Shen, M. Hampson, F.S. Winstanley et al., Potential use and challenges of functional connectivity mapping in intractable epilepsy, Front. Neurol. 4, 39 (2013) [CrossRef] [Google Scholar]
  4. K. Lehnertz, S. Bialonski, M.T. Horstmann, D. Krug, A. Rothkegel, M. Staniek et al., Synchronization phenomena in human epileptic brain networks, J. Neurosci. Methods 183, 42 (2009) [CrossRef] [PubMed] [Google Scholar]
  5. B.C. Bernhardt, S. Hong, A. Bernasconi, N. Bernasconi, Imaging structural and functional brain networks in temporal lobe epilepsy, Front. Hum. Neurosci. 7, 624 (2013) [CrossRef] [Google Scholar]
  6. L. Leistritz, B. Pester, A. Doering, K. Schiecke, F. Babiloni, L. Astolfi et al., Time-variant partial directed coherence for analysing connectivity: a methodological study, Philos. Trans. A: Math. Phys. Eng. Sci. 371, 20110616 (2013) [CrossRef] [Google Scholar]
  7. C.W.J. Granger, Investigating causal relations by econometric models and cross-spectral methods, Econometrica 37, 414 (1969) [Google Scholar]
  8. T. Milde, L. Leistritz, L. Astolfi, W.H. Miltner, T. Weiss, F. Babiloni et al., A new Kalman filter approach for the estimation of high-dimensional time-variant multivariate AR models and its application in analysis of laser-evoked brain potentials, NeuroImage 50, 960 (2010) [CrossRef] [Google Scholar]
  9. K.J. Blinowska, Review of the methods of determination of directed connectivity from multichannel data, Med. Biol. Eng. Comput. 49, 521 (2011) [Google Scholar]
  10. T. Schreiber, Measuring information transfer, Phys. Rev. Lett. 85, 461 (2000) [CrossRef] [PubMed] [Google Scholar]
  11. R. Vicente, M. Wibral, M. Lindner, G. Pipa, Transfer entropy – a model-free measure of effective connectivity for the neurosciences, J. Comput. Neurosci. 30, 45 (2011) [Google Scholar]
  12. P. Wollstadt, M. Martinez-Zarzuela, R. Vicente, F.J. Diaz-Pernas, M. Wibral, Efficient transfer entropy analysis of non-stationary neural time series, PLOS ONE 9, e102833 (2014) [CrossRef] [Google Scholar]
  13. G. Sugihara, R. May, H. Ye, C.H. Hsieh, E. Deyle, M. Fogarty et al., Detecting causality in complex ecosystems, Science 338, 496 (2012) [CrossRef] [PubMed] [Google Scholar]
  14. E.R. Deyle, M. Fogarty, C.H. Hsieh, L. Kaufman, A.D. MacCall, S.B. Munch et al., Predicting climate effects on Pacific sardine, Proc. Natl. Acad. Sci. USA 110, 6430 (2013) [CrossRef] [Google Scholar]
  15. E.H. van Nes, M. Scheffer, V. Brovkin, T.M. Lenton, H. Ye, E. Deyle et al., Causal feedbacks in climate change, Nat. Clim. Change 5, 445 (2015) [CrossRef] [Google Scholar]
  16. K. Schiecke, B. Pester, D. Piper, F. Benninger, M. Feucht, L. Leistritz et al., Nonlinear directed interactions between HRV and EEG activity in children with TLE, IEEE Trans. Biomed. Eng. 63, 2497 (2016) [CrossRef] [Google Scholar]
  17. K. Schiecke, M. Wacker, D. Piper, F. Benninger, M. Feucht, H. Witte, Time-variant, frequency-selective, linear and nonlinear analysis of heart rate variability in children with temporal lobe epilepsy, IEEE Trans. Biomed. Eng. 61, 1798 (2014) [CrossRef] [Google Scholar]
  18. H. Mayer, F. Benninger, L. Urak, B. Plattner, J. Geldner, M. Feucht, EKG abnormalities in children and adolescents with symptomatic temporal lobe epilepsy, Neurology 63, 324 (2004) [CrossRef] [Google Scholar]
  19. R. Oostenveld, P. Fries, E. Maris, J.M. Schoffelen, FieldTrip: open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data, Comput. Intell. Neurosci. 2011, 156869 (2011) [Google Scholar]
  20. D. Piper, R. Strungaru, H. Witte, Artefact removal approach for epileptic EEG data, UPB Sci. Bull. Ser. C 77, 213 (2015) [Google Scholar]
  21. N. Rehman, D.P. Mandic, Multivariate empirical mode decomposition, Proc. R. Soc. A: Math. Phys. Eng. Sci. 466, 1291 (2010) [CrossRef] [Google Scholar]
  22. N.E. Huang, Z. Shen, S.R. Long, M.L.C. Wu, H.H. Shih, Q.N. Zheng et al., The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis, Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci. 454, 903 (1998) [CrossRef] [Google Scholar]
  23. M. Wacker, H. Witte, Time–frequency techniques in biomedical signal analysis. A tutorial review of similarities and differences, Method Inform. Med. 52, 279 (2013) [CrossRef] [Google Scholar]
  24. P. Flandrin, G. Rilling, P. Goncalves, Empirical mode decomposition as a filter bank, IEEE Signal Proc. Lett. 11, 112 (2004) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. N.U. Rehman, D.P. Mandic, Filter bank property of multivariate empirical mode decomposition, IEEE Trans. Signal Process. 59, 2421 (2011) [CrossRef] [Google Scholar]
  26. J. Theiler, S. Eubank, A. Longtin, B. Galdrikian, J.D. Farmer, Testing for nonlinearity in time-series – the method of surrogate data, Physica D 58, 77 (1992) [NASA ADS] [CrossRef] [Google Scholar]
  27. D. Piper, K. Schiecke, B. Pester, F. Benninger, M. Feucht, H. Witte, Time-variant coherence between heart rate variability and EEG activity in epileptic patients: an advanced coupling analysis between physiological networks, New J. Phys. 16, 115012 (2014) [CrossRef] [Google Scholar]
  28. B. Efron, R.J. Tibshirani, An Introduction to the Bootstrap (Chapman & Hall, New York, 1993) [Google Scholar]
  29. P.J. Franaszczuk, G.K. Bergey, Application of the directed transfer function method to mesial and lateral onset temporal lobe seizures, Brain Topogr. 11, 13 (1998) [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  30. Y.K. Dai, W.B. Zhang, D.L. Dickens, B. He, Source connectivity analysis from MEG and its application to epilepsy source localization, Brain Topogr. 25, 157 (2012) [CrossRef] [Google Scholar]
  31. C. Wilke, G.A. Worrell, B. He, Connectivity analysis of ictal activity from electrocorticography, Epilepsia 50, 35 (2009) [Google Scholar]
  32. G. Bettus, F. Wendling, M. Guye, L. Valton, J. Regis, P. Chauvel et al., Enhanced EEG functional connectivity in mesial temporal lobe epilepsy, Epilepsy Res. 81, 58 (2008) [CrossRef] [Google Scholar]
  33. A.E.P. Villa, I.V. Tetko, Cross-frequency coupling in mesiotemporal EEG recordings of epileptic patients, J. Physiol. 104, 197 (2010) [Google Scholar]
  34. H. Stefan, F.H. Lopes da Silva, Epileptic neuronal networks: methods of identification and clinical relevance, Front. Neurol. 4, 8 (2013) [CrossRef] [Google Scholar]
  35. M. Winterhalder, B. Schelter, W. Hesse, K. Schwab, L. Leistritz, D. Klan et al., Comparison directed of linear signal processing techniques to infer interactions in multivariate neural systems, Signal Process. 85, 2137 (2005) [CrossRef] [Google Scholar]
  36. D. Prichard, J. Theiler, Generating surrogate data for time-series with several simultaneously measured variables, Phys. Rev. Lett. 73, 951 (1994) [NASA ADS] [CrossRef] [Google Scholar]
  37. S. Haufe, V.V. Nikulin, K.R. Muller, G. Nolte, A critical assessment of connectivity measures for EEG data: a simulation study, NeuroImage 64, 120 (2013) [CrossRef] [Google Scholar]
  38. D. Sakellariou, A.M. Koupparis, V. Kokkinos, M. Koutroumanidis, G.K. Kostopoulos, Connectivity measures in EEG microstructural sleep elements, Front. Neuroinform. 10, 5 (2016) [CrossRef] [Google Scholar]
  39. A. Papana, C. Kyrtsou, D. Kugiumtzis, C. Diks, Simulation study of direct causality measures in multivariate time series, Entropy 15, 2635 (2013) [CrossRef] [Google Scholar]
  40. K. Lehnertz, H. Dickten, Assessing directionality and strength of coupling through symbolic analysis: an application to epilepsy patients, Philos. Trans. A: Math. Phys. Eng. Sci. 373, 20140094 (2015) [CrossRef] [Google Scholar]
  41. R.P. Bartsch, K.K. Liu, A. Bashan, P. Ivanov, Network physiology: how organ systems dynamically interact, PLOS ONE 10, e0142143 (2015) [CrossRef] [Google Scholar]
  42. L. Faes, D. Marinazzo, F. Jurysta, G. Nollo, Linear and non-linear brain-heart and brain-brain interactions during sleep, Physiol. Meas. 36, 683 (2015) [CrossRef] [Google Scholar]
  43. G. Pfurtscheller, M. Walther, G. Bauernfeind, R.J. Barry, H. Witte, G.R. Muller-Putz, Entrainment of spontaneous cerebral hemodynamic oscillations to behavioral responses, Neurosci. Lett. 566, 93 (2014) [CrossRef] [Google Scholar]
  44. P.C. Ivanov, R.P. Bartsch, Network physiology: mapping interactions between networks of physiologic networks, in Networks of Networks: The Last Frontier of Complexity, edited by G. D'Agostino, A. Scala (Springer International Publishing, Cham, 2014), pp. 203–222 [CrossRef] [Google Scholar]

Cite this article as: Karin Schiecke, Britta Pester, Diana Piper, Martha Feucht, Franz Benninger, Herbert Witte, Lutz Leistritz, Advanced nonlinear approach to quantify directed interactions within EEG activity of children with temporal lobe epilepsy in their time course, EPJ Nonlinear Biomed. Phys. 5, 3 (2017)

All Figures

thumbnail Fig. 1

General design of processing scheme. Investigated data, preprocessing, and the main characteristics of the applied approaches as well as statistical measures are given.
In the text
thumbnail Fig. 2

Time courses of original data and extracted EEG components of one child (left side focus). Investigated electrode positions and focus of seizure are given in (A); example of original EEG recording at ipsilateral focus area electrode (blue), contralateral focus area electrode (red), ipsilateral near to focus area electrode (green), as well as ipsilateral far away from focus area electrode (cyan) are given in (B), and extracted δ- and α-IMFs are shown in (C). Black bold line designates onset of seizure at 5 min.
In the text
thumbnail Fig. 3

Schematic overview of investigated CCMs. Interactions within EEG activity, within δ-EEG activity, as well as within α-EEG activity are examined at (A) ipsilateral vs. contralateral focus area positions, (B) ipsilateral near to focus area positions, and (C) ipsilateral far away from focus area positions for all children. Electrode positions are given for left-sided focus (note different locations for right-sided seizures in brackets).
In the text
thumbnail Fig. 4

MVAR results of one child. Multivariate AR parameter matrices during preictal (A), ictal (B), and postictal periods (C) are shown, illustrating the dominance of all diagonal entries. Furthermore, estimated time series of electrodes T3 (D) and T4 (E) are depicted, where the blue line represents the use of univariate estimation (only one channel is used) and the gray line depicts the use of multivariate estimation (all channels are included to the model). Specific time points of MVAR parameter shown in (A) to (C) are marked in (D) and (E) by dashed red lines.
In the text
thumbnail Fig. 5

Results of the investigation of increasing library length L on the estimation of CCM. Mean results of all children (K = 18) are shown. CCM and tubes of 95% CI of bootstrapping approach, bold lines designating the statistical thresholds by surrogate data approach, as well as appropriate library length of L = 4 s (vertical thin line) are shown.
In the text
thumbnail Fig. 6

Results of time-varying interval-based investigation of CCM of the ipsilateral vs. contralateral focus area. A sliding window of 4 s (=256 data points) is used. In (A) and (B), both directions of interval-based results of CCM of EEG activity (black and gray), δ-EEG activity (blue and cyan), as well as α-EEG activity (red and magenta) are shown (mean result of all children; color code of direction according to Fig. 3). Gray rectangle marks onset and median length of seizure.
In the text
thumbnail Fig. 7

Results of time-varying interval-based investigation of CCM in dependence to the investigated electrode positions. Only one direction of interaction is shown (ipsilateral focus area to other positions). In (A) to (C), interval-based results of CCM of EEG activity (black), δ-EEG activity (blue), as well as α-EEG activity (red) are shown for all three different investigated electrode positions (mean result of all children; color code according to Fig. 3). Gray rectangle marks onset and median length of seizure.
In the text
thumbnail Fig. 8

Results of statistical evaluation of time-varying interval-based investigation of CCM in dependence to the investigated electrode positions. Only one direction of interaction is shown (ipsilateral focus area to other positions). In (A) to (C), interval-based results of CCM of EEG activity (black), δ-EEG activity (blue), as well as α-EEG activity (red) are shown for all investigated electrode positions (mean result of all children). Confidence tubes achieved by bootstrapping and statistical threshold for significant CCM values (thin lines) are given according to the color code (Fig. 3). Gray rectangle marks onset and median length of seizure.
In the text